5 класс, Школьный уровень

1 ВАРИАНТ

1) Выразите числа 5, 30 и 55, используя четыре цифры 5, знаки арифметических действий и скобки.
2) Восстановите цифры и знаки действия:

3) В сказочном озере плавает сказочная лилия. Эта лилия за сутки вдвое увеличивает свои размеры и полностью заполняет озеро за 137 суток. За какое причём 5 из них – красные, а 6 – розы. Какое число белых гвоздик может быть в букете?

4) Девочка заменила каждую букву в своём имени её номером в русском алфавите и получила 2011533. Как её зовут?
5) В букете 11 цветов, причём 5 из них – красные, а 6 – розы. Какое число белых гвоздик может быть в букете?

2 ВАРИАНТ.
1) 15 шариков можно сложить в виде треугольника, но нельзя в виде квадрата — одного шарика не хватает. Из какого числа шариков, не превосходящего 50, можно сложить как треугольник, так и квадрат?
2) Найдите наибольшее и наименьшее трёхзначное число, делящееся на 6 и имеющее в своей записи цифру 7.
3) В коробке лежат скрепки трёх цветов. Петя знает, что если вынуть наугад любые 100 скрепок из коробки, то среди них обязательно найдутся скрепки всех трёх видов. Какое наибольшее количество скрепок может быть в коробке у Пети?
4) В январе некоторого года было 4 понедельника и 4 пятницы. Каким днём могло быть 20-е число этого месяца?
5) Разрежьте фигуру, изображенную на рисунке, на 4 равные части.

6) Мне удалось, взяв по 2 раза цифры 1,2,3 и 4, написать восьмизначное число, у которого между единицами стоит одна цифра, между двойками — две, между тройками — три, между четвёрками — четыре. Какое это число?

3 ВАРИАНТ

1) Не пользуясь калькулятором, выполнить указанные действия, записав подробно решение:90102-(((700100100-79655100):875-628990)*(10010-2950)-9055130):6894+603
2) Восстановите умножение двух чисел, заменив звёздочки цифрами. Прокомментируйте своё решение.

3) Из 75 одинаковых по виду колец одно отличается по весу. Двумя взвешиваниями на чашечных весах без гирь определите, легче оно или тяжелее. Опишите процедуру взвешивания.
4) В ящике лежит 100 шариков: 30 красных,30 синих,30 зелёных, остальные белые и чёрные. Какое наименьшее количество шариков необходимо вынуть, чтобы достать 20 шариков какого-либо цвета?
5) Путешественник может пройти 1247 км за 29 дней, находясь каждый день в пути по 7 часов. Какое расстояние он пройдёт за 21 день, если ежедневно будет находиться в пути 10 часов?

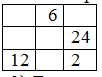
Задача 1: Если поместить каждую из цифр 2,4,5,6,9 ровно в один из прямоугольников данного примера на вычитание, то какая наименьшая разность может получиться?

Задача 2: На каждые три девочки в классе приходится два мальчика. Если всего в классе тридцать учеников, то сколько из них девочек?

Задача 3: В магазине положили картофель в пакеты по 3 и 5 кг. Всего получили 24 пакета. Вес всех пакетов по 5 кг равен весу всех пакетов по 3 кг. Сколько было пакетов по 3 кг?

Задача 4: Хулиган Вася вырезал из шахматной доски квадрат 4 × 4, из угла получившегося квадрата он вырезал квадрат 2 × 2. Сможет ли он разрезать получившийся уголок по линиям доски на четыре одинаковые части?

Задача 5: Заменить звездочки цифрами так, чтобы получилось верное равенство: *** · 9* = *2**. Найти все решения. Первые звездочки в числах заменяются на цифры, отличные от нуля.

4 ВАРИАНТ

1) Брюки стоят 700 р. Пальто в 6 раз дороже, чем брюки, а ботинки в 6 раз дешевле пальто. Сколько стоят ботинки?

2) В клетки квадрата запишите недостающие числа так, чтобы произведение чисел на любой вертикали и горизонтали было равно 480.

3) Если школьник купит 11 тетрадей, то у него останется 5 рублей. А на 15 тетрадей у него не хватает 7 рублей. Сколько денег у школьника?

4) Как, имея два сосуда вместимостью 5 л. и 7 л., налить из водопроводного крана 6 л.?

5) Как разрезать прямоугольник, длина которого 16 см, а ширина 9 см, на две равные части, из которых можно составить квадрат?

5 ВАРИАНТ

1) Найдите наибольшее целое число, которое при делении на 13 с остатком дает частное 17.

2) Андрей купил 3 стакана орехов, а Борис – два стакана. К ним присоединился Саша, и они разделили все орехи поровну. При расчете оказалось, что Саша должен уплатить товарищам 20 рублей. Сколько денег из этой суммы должен получить Андрей и сколько Борис?

3) Беговую дорожку круглой формы один спортсмен пробегает за 12 мин., другой – за 16 мин. Через сколько времени один спортсмен догонит другого, если они начинают бежать одновременно из одной точки в одном направлении?

4) Из числа 12345678910111213…5657585960 вычеркните 100 цифр так, чтобы оставшееся число стало наибольшим.

5) Чебурашка живет в высотном здании. На каком этаже находится его квартира, если:

• поднявшись на лифте с этажа, на котором находится его квартира, на 20 этажей, он оказался выше 62-го, но ниже 71-го этажа;
• спустившись с этажа, на котором находится его квартира, на 15 этажей, он оказался выше 30-го, но ниже 40-го этажа;
• поднявшись с этажа, на котором находится его квартира, на 29 этажей, он оказался выше 67-го, но ниже 78-го этажа;
• спустившись с этажа, на котором находится его квартира, на 38 этажей, он оказался выше 9-го, но ниже 12-го этажа.

6 ВАРИАНТ

1) Вычислите наиболее простым способом: 19991999 * 2000 – 19991998 * 2000.

2) Шоколадка состоит из 6х4 долек. Сколько разломов потребуется сделать, чтобы разделить ее на 24 части? Накладывать части друг на друга не разрешается.

3) Гриша пошел с отцом в тир. Уговор был такой: Гриша делает 5 выстрелов и за каждое попадание в цель получает право сделать еще 2 выстрела. Гриша сделал 17 выстрелов. Сколько раз он попал в цель?

4) В клетках таблицы, содержащей 4 строки и 7 столбцов, расставьте натуральные числа так, чтобы их сумма в каждой строке была равна 28, а в каждом столбце 15. Можно ли осуществить требуемое?

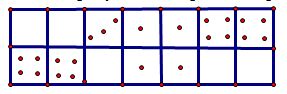
7 ВАРИАНТ

1)  Какие числа нужно поставить в примере вместо знаков, если известно, что остаток наибольший из возможных?

 
 

2) Начертите двенадцатиугольник так, чтобы соединив его вершины через одну, получить шестиугольник, площадь которого больше, чем площадь двенадцатиугольника.

3) В коробке лежат 7 костяшек домино из одного комплекта, но границ между ними не видно. Нарисуйте, где проходят границы между костяшками, и объясните свой ответ.

4) Олегу подарили игрушечного робота. Наблюдая за ним в течение долгого времени, он заметил, что:

• если сейчас робот кивает, то через минуту он моргает;
• если сейчас робот топает, то через минуту он хлопает;
• если сейчас робот пищит, то через минуту он кивает;
• если сейчас робот трещит, то через минуту он пищит;
• если сейчас робот моргает, то через минуту он топает;
• если сейчас робот хлопает, то через минуту он трещит.

Сейчас робот пищит. Что он будет делать через 40 минут?

5) Путешественник Вася, живущий в 50 км от места проведения Турнира Архимеда, решил поехать на Турнир на велосипеде. Рассчитав время, он проехал первые 10 км с запланированной скоростью, но затем велосипед сломался, и Васе пришлось пойти пешком. Через некоторое время Васе повезло, и последние 24 км он ехал на попутной машине. Удалось ли Васе приехать на Турнир к запланированному сроку, если скорость Васиной ходьбы была в 2,5 раза меньше скорости велосипеда, а скорость машины – в 6 раз больше?

6) Для двух натуральных чисел А и В вычислили их сумму С и произведение D. Затем для чисел C и D нашли их сумму E и произведение F. Из чисел E и F – одно оказалось нечетным. Какое именно и почему?